Components¶

The theta package comes with the following modules:

RTBM (theta.rtbm)
Model (theta.model)
Layers (theta.layers)
Minimizers (theta.minimizer)
Activations (theta.activations)
Initializers (theta.initializers)
Cost functions (theta.costfunctions)
Stopping conditions (theta.stopping)

These modules provide all the required components to train Riemann-Theta Boltzmann Machines for probability density estimation, regression and classification.

RTBM¶

The theta.rtbm module contains the definition of class RTBM. This object provides the simplest interface to the parameters of the RTBM and to the probability and expectation values.

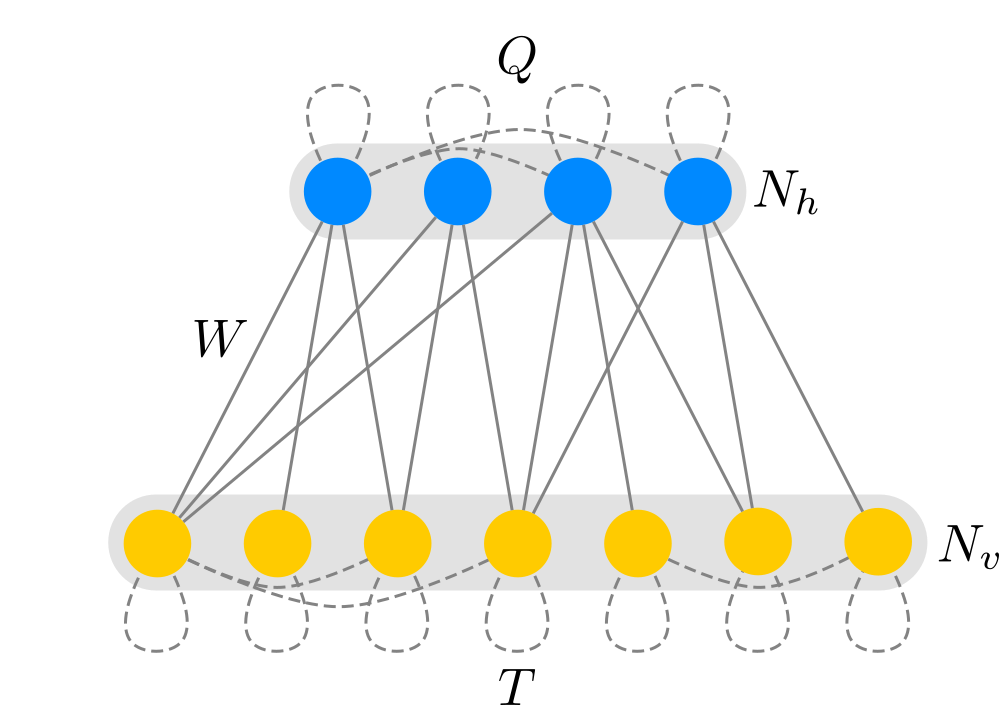
Schematically, the RTBM is given by the network configuration

where \(T\) is the connection matrix of the visible sector with \(N_v\) visible units, \(Q\) of the hidden sector with \(N_h\) hidden units and \(W\) the inter-connections.

class theta.rtbm.RTBM(visible_units, hidden_units, mode=0, init_max_param_bound=2, random_bound=1, phase=1, diagonal_T=False)¶

This class implements the Riemann-Theta Boltzmann Machine.

Parameters:

visible_units (int) – number of visible units.
hidden_units (int) – number of hidden units.
mode (theta.rtbm.RTBM.Mode) – set the working mode among: probability mode (Mode.Probability), log of probability (Mode.LogProbability) and expectation (Mode.Expectation), see theta.rtbm.RTBM.Mode.
init_max_param_bound (float) – maximum value allowed for all parameters during the CMA-ES minimization.
random_bound (float) – selects the maximum random value for the Schur complement initialization.
phase (complex) – number which multiplies w and bh phase=1 for Phase I and phase=1j for Phase II.
diagonal_T (bool) – force T diagonal, by default T is symmetric.
check_positivity (bool) – enable positivity condition check in set_parameters.

Properties (setters and getters):

mode (theta.rtbm.RTBM.Mode) - sets and returns the RTBM mode.

bv (numpy.array) - sets and returns the Bv.

t (numpy.array) - sets and returns the T.

bh (numpy.array) - sets and returns the Bh.

w (numpy.array) - sets and returns the W.

q (numpy.array) - sets and returns the Q.

Example

from theta.rtbm import RTBM
m = RTBM(1, 2)  # allocates a RTBM with Nv=1 and Nh=2
print(m.size()) # returns the total number of parameters
output = m(x)   # evaluate prediction

predict(x)¶

Performs prediction with the trained model. This method has a shortcut defined by the parenthese operator, i.e. model.predict(x) and model(x) are equivalent.

Parameters:	x (numpy.array) – input data, shape (Nv, Ndata)
Returns:	evaluates Model predictions.
Return type:	numpy.array

random_init(bound)¶

Random initializer which satisfies the Schur complement positivity condition. If diagonal_T=True the initial Q and T are diagonal and W is set to zero.

Parameters:	bound (float) – the maximum value for the random matrix X used by the Schur complement.

mean()¶

Computes the first moment estimator (mean).

Returns:	the mean of the probability distribution.
Return type:	float
Raises:	`theta.rtbm.AssertionError` – if `mode` is not `theta.rtbm.RTBM.Mode.Probability`.

size()¶

Returns:	the size of the RTBM.
Return type:	int

get_parameters()¶

Returns:	flat array with all RTBM parameters.
Return type:	numpy.array

get_gradients()¶

Returns:	flat array with calculated gradients [Gbh,Gbv,Gw,Gt,Gq].
Return type:	numpy array

set_bounds(param_bound)¶

Sets the parameter bound for each parameter.

Parameters:	param_bound (float) – the maximum absolute value for parameter variation.

get_bounds()¶

Returns:	two arrays with min and max of each parameter for the GA.
Return type:	list of numpy.array

Model¶

The theta package provide a dedicated container for RTBM probability mixtures models and theta neural networks (TNNs) through the class Model stored in theta.model.

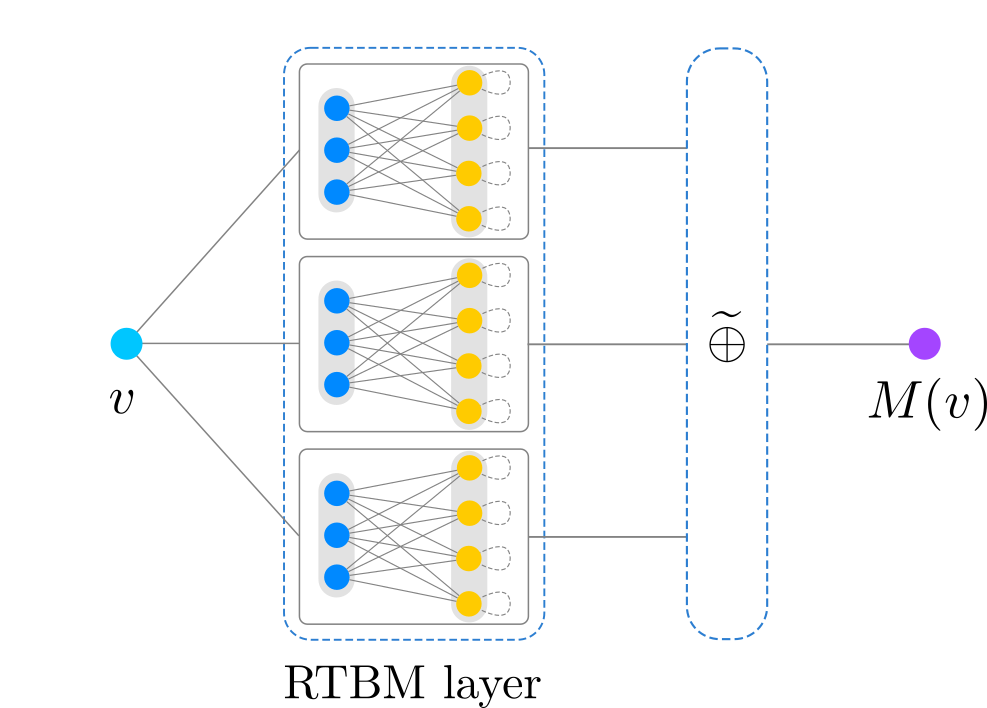
This module allows the concatenation of objects for building mixture model based on multiple RTBMs and a final NormAddLayer, such as:

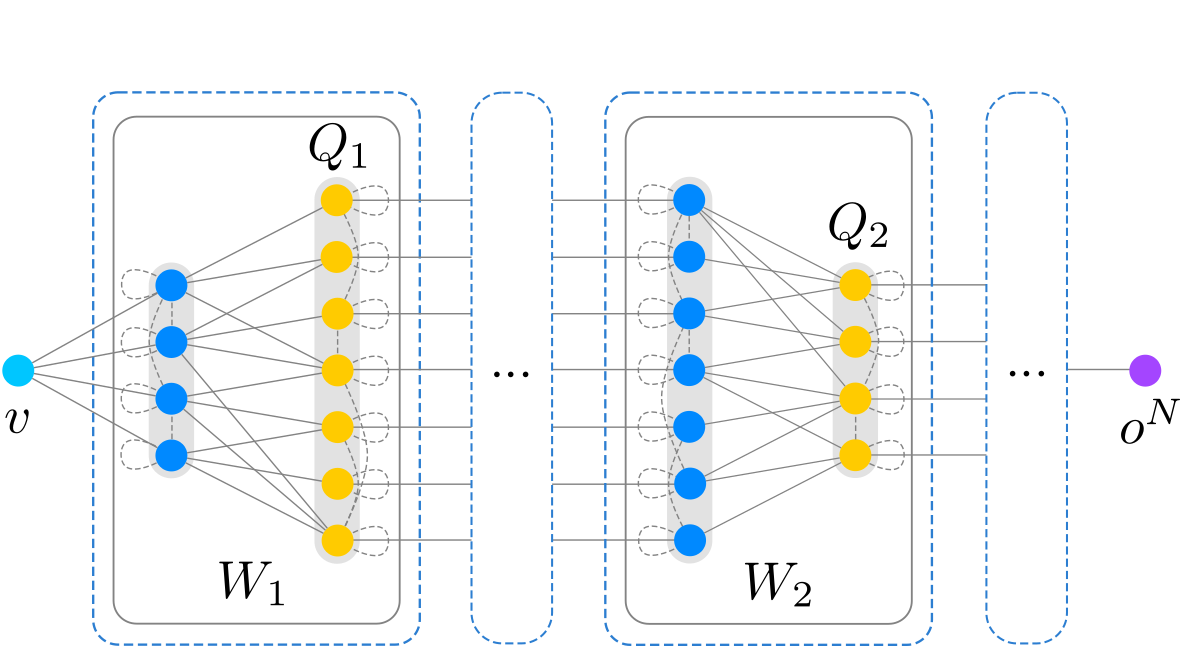
and the possibility to build TNNs, e.g.:

Further information about the implemented layers for the TNNs are listed in the Layers section of this document.

class theta.model.Model¶

The model class which holds layer for building mixture models and theta neural networks.

Example

from theta.theta import Model
from theta.layers import ThetaUnitLayer, AddNormLayer
m = Model()  # allocates a RTBM with Nv=1 and Nh=2
m.add(ThetaUnitLayer(1,2))
m.add(NormAddLayer(2,1))

predict(x)¶

Performs prediction with the trained model. This method has a shortcut defined by the parenthese operator, i.e. model.predict(x) and model(x) are equivalent.

Parameters:	x (numpy.array) – input data, shape (Nv, Ndata)
Returns:	evaluates Model predictions.
Return type:	numpy.array

add(layer)¶

Add layer to the model instance.

Parameters:	layer (theta.layers) – any layer implemented in theta.layers (Layers).

Warning

The layer input size must match the output size of previous layer!

size()¶

Returns:	the size of the RTBM.
Return type:	int

get_parameters()¶

Collects all parameters and returns a flat array.

Returns:	flat array with current matrices weights.
Return type:	numpy.array

get_gradients()¶

Collects all gradients and returns a flat array.

Returns:	flat array with calculated gradients.
Return type:	numpy array

get_layer(N)¶

Parameters:	N (int) – the layer number.
Returns:	returns the N-th layer stored in the model
Return type:	theta.layers

get_bounds()¶

Returns:	two arrays with min and max of each parameter of all layers.
Return type:	list of numpy.array

gradient_check(g, x, epsilon)¶

Performs numerical check of gth gradient.

Parameters:	g (int) – id of gradient to check. x (numpy.array) – input data shape (Ninput, Ndata). epsilon (float) – infinitesimal variation of parameter.
Returns:	the numerical and analytical gradients.
Return type:	floats

Layers¶

The theta package implements the following layers:

Theta Probability Unit: provides a layer with multiple RTBMs setup in probability mode. This layer is used to build probability and mixture models.
Theta Diagonal Expectation Unit: A layer consisting of a RTBM in expectation mode with diagonal \(Q\). This layer is suitable for regression and classification applications, and can be combined with other layers into a deep model.
Normalized Additive: performs a weighted sum of the inputs. This layer guarantees a positive and normalized output and is used to build mixture models.
Linear: a standard linear layer for testing and benchmarking purposes.
Non-Linear: a non linear layer for testing and benchmarking purposes.

All layers are inherited from the theta.layers.Layer class, so custom layers can be implemented by extending that class.

Theta Probability Unit¶

class theta.layers.ThetaUnitLayer(Nin, Nout, Nhidden=1, init_max_param_bound=2, random_bound=1, phase=1, diagonal_T=False)¶

Allocate a Theta Unit Layer working in probability mode

Parameters:

Nin (int) – number of input nodes
Nout (int) – number of output nodes (i.e. # of RTBMs)
Nhidden (int) – number of hidden layers per RTBM
init_max_param_bound (float) – maximum bound value for CMA
random_bound (float) – the maximum value for the random matrix X used by initialization
phase (complex) – number which multiplies w and bh phase=1 for Phase I and phase=1j for PhaseII.
diagonal_T (bool) – force T diagonal, by default T is symmetric.

get_unit(N)¶

Return the singular RTBM unit.

Parameters:	N (int) – the Nth RTBM unit.
Returns:	the Nth RTBM unit.
Return type:	theta.rtbm.RTBM

get_parameters()¶

Returns:	the parameters as a flat array [b,w,q].
Return type:	numpy.array

get_bounds()¶

Returns:	two arrays with min and max of each parameter of the layer for the GA.
Return type:	list of numpy.array

size()¶

Returns:	total number of parameters.
Return type:	int

get_gradients()¶

Returns:	gradients for all RTBM units as a flat array.
Return type:	numpy.array

Theta Diagonal Expectation Unit¶

class theta.layers.DiagExpectationUnitLayer(Nin, Nout, W_init=<theta.initializers.glorot_uniform object>, B_init=<theta.initializers.null object>, Q_init=<theta.initializers.uniform object>, param_bound=16, phase=1)¶

A layer of log-gradient theta units.

Parameters:

Nin (int) – number of inputs.
Nout (int) – number of outputs.
W_init (theta.initializers) – random initialization for W
B_init (theta.initializers) – random initialization for B
Q_init (theta.initializers) – random initialization for Q
param_bound (float) – maximum value alowed for the optimization via genetic optimizer.
phase (complex) – the RTBM phase (default=1)

show_activation(N, bound=2)¶

Plots the Nth activation function on [-bound,+bound].

Parameters:	N (int) – the Nth activation function bound (float) – min/max value for the plot.

get_parameters()¶

Returns:	the parameters as a flat array [bh,w,q]
Return type:	numpy.array

get_bounds()¶

Returns:	two arrays with min and max of each parameter of the layer for the GA.
Return type:	list of numpy.array

get_gradients()¶

Returns:	B, W and Q gradients as a flat array
Return type:	numpy.array

size()¶

Returns:	total number of parameters.
Return type:	int

Normalized Additive¶

class theta.layers.NormAddLayer(Nin, Nout, W_init=<theta.initializers.null object>, param_bound=10)¶

Linearly combines inputs with outputs normalized by sum of weights. Weights are exponentiated.

\[M(v) = \frac{1}{\sum_{i=1}^N e^{\omega_i}} \sum_{i=1}^{N} e^{\omega_i} P^{(i)}(v)\]

Parameters:	Nin (int) – number of input nodes. Nout (int) – number of output nodes. W_init (theta.initializers) – random initialization for weights. param_bound (float) – maximum value alowed for the optimization via genetic optimizer.

get_parameters()¶

Returns:	the parameters as a flat array [w].
Return type:	numpy.array

get_gradients()¶

Returns:	W gradients as a flat array
Return type:	numpy.array

get_bounds()¶

Returns:	two arrays with min and max of each parameter of the layer for the GA.
Return type:	list of numpy.array

size()¶

Returns:	total number of parameters.
Return type:	int

Linear¶

class theta.layers.Linear(Nin, Nout, W_init=<theta.initializers.glorot_uniform object>, B_init=<theta.initializers.null object>, param_bound=10)¶

Linear layer.

Parameters:	Nin (int) – number of inputs. Nout (int) – number of outputs. W_init (theta.initializers) – random initialization for weights. B_init (theta.initializers) – random initialization for biases. param_bound (float) – maximum value alowed for the optimization via genetic optimizer.

get_parameters()¶

Returns:	the parameters as a flat array [b,w].
Return type:	numpy.array

get_gradients()¶

Returns:	B and W gradients as a flat array
Return type:	numpy.array

get_bounds()¶

Returns:	two arrays with min and max of each parameter of the layer for the GA.
Return type:	list of numpy.array

size()¶

Returns:	total number of parameters.
Return type:	int

Non-Linear¶

class theta.layers.NonLinear(Nin, Nout, activation=<class 'theta.activations.tanh'>, W_init=<theta.initializers.glorot_uniform object>, B_init=<theta.initializers.null object>, param_bound=10)¶

Non-Linear layer.

Parameters:	Nin (int) – number of inputs. Nout (int) – number of outputs. activation (theta.activations) – the non-linear activation function. W_init (theta.initializers) – random initialization for weights. B_init (theta.initializers) – random initialization for biases. param_bound (float) – maximum value alowed for the optimization via genetic optimizer.

get_parameters()¶

Returns:	the parameters as a flat array [b,w].
Return type:	numpy.array

get_gradients()¶

Returns:	B and W gradients as a flat array
Return type:	numpy.array

get_bounds()¶

Returns:	two arrays with min and max of each parameter of the layer for the GA.
Return type:	list of numpy.array

size()¶

Returns:	total number of parameters.
Return type:	int

Minimizers¶

The theta package provides two minimizers:

CMA-ES (evolutionary strategy)
Stochastic Gradient Descent (SGD)

We also provide the BFGS optimizer for testing purposes.

Evolutionary algorithm¶

class theta.minimizer.CMA(parallel=False, ncores=0)¶

Implements the GA using CMA-ES library (cma package). This class provides a basic CMA-ES implementation for RTBMs.

Parameters:	parallel (bool) – if set to True the algorithm uses multi-processing. ncores (int) – limit the number of cores when `parallel=True`.

train(cost, model, x_data, y_data=None, tolfun=1e-11, popsize=None, maxiter=None, use_grad=False)¶

Trains the model using the custom cost function.

Parameters:	cost (theta.costfunctions) – the cost function. model (theta.model.Model or theta.rtbm.RTBM) – the model to be trained. x_data (numpy.array) – the support data with shape (Nv, Ndata). y_data (numpy.array) – the target prediction. tolfun (float) – the maximum tolerance of the cost function fluctuation to stop the minimization. popsize (int) – the population size. maxiter (int) – the maximum number of iterations. use_grad (bool) – if True the gradients for the cost and model are used in the minimization.
Returns:	the optimal parameters
Return type:	numpy.array

Note

The parameters of the model are changed by this algorithm.

Gradient descent¶

class theta.minimizer.SGD¶

Stochastic gradient descent.

train(cost, model, x_data, y_data=None, validation_split=0, validation_x_data=None, validation_y_data=None, stopping=None, scheme=None, maxiter=100, batch_size=0, shuffle=False, lr=0.001, decay=0, momentum=0, nesterov=False, noise=0, cplot=True)¶

Trains the given model with stochastic gradient descent methods

Parameters:	cost (theta.costfunctions) – the cost fuction class model (theta.rtbm.Model or theta.model.Model) – the model to be trained x_data (numpy.array) – the target data support y_data (numpy.array) – the target data prediction validation_split (float) – fraction of data used for validation only validation_x_data (numpy.array) – external set of validation support validation_y_data (numpy.array) – external set of validation target stopping (theta.stopping) – the stopping class (see `theta.stopping`) scheme (theta.gradientscheme) – the SGD method (Ada, RMSprop, see Gradient descent schemes) maxiter (int) – maximum number of allowed iterations batch_size (int) – the batch size shuffle (bool) – shuffle the data on each iteration lr (float) – learning rate decay (float) – learning rate decay rate momentum (float) – add momentum nesterov (bool) – add nesterov momentum noise (bool) – add gaussian noise cplot (bool) – if True shows the cost function evolution
Returns:	iterations, cost and validation functions
Return type:	dictionary

Note

The parameters of the model are changed by this algorithm.

class theta.minimizer.BFGS¶

Implements the BFGS method

train(cost, model, x_data, y_data=None, tolfun=1e-11, maxiter=100)¶

Parameters:	cost (theta.costfunctions) – the cost function. model (theta.model.Model or theta.rtbm.RTBM) – the model to be trained. x_data (numpy.array) – the support data with shape (Nv, Ndata). y_data (numpy.array) – the target prediction. tolfun (float) – the maximum tolerance of the cost function fluctuation to stop the minimization. popsize (int) – the population size. maxiter (int) – the maximum number of iterations.
Returns:	the optimal parameters
Return type:	numpy.array

Note

The parameters of the model are changed by this algorithm.

Gradient descent schemes¶

class theta.gradientschemes.adagrad(epsilon=1e-05)¶

The Adagrad scheme.

Parameters:	epsilon (float) – smoothing term to avoid division by zero

getupdate(G, lr)¶

Get updates.

Parameters:	G (numpy.array) – gradients lr (float) – learning rate
Returns:	the updated gradient.
Return type:	numpy.array

class theta.gradientschemes.RMSprop(rate=0.9, epsilon=1e-05)¶

The RMS propagation scheme.

Parameters:	rate (float) – weighting of the previous squared gradient expectation value epsilon (float) – smoothing term to avoid division by zero

getupdate(G, lr)¶

Get updates.

Parameters:	G (numpy.array) – gradients lr (float) – learning rate
Returns:	the updated gradient.
Return type:	numpy.array

class theta.gradientschemes.adadelta(rate=0.9, epsilon=1e-05)¶

The Adadelta scheme.

Parameters:	rate (float) – weighting of the previous squared gradient expectation value epsilon (float) – smoothing term to avoid division by zero

getupdate(G, lr)¶

Get updates.

Parameters:	G (numpy.array) – gradients lr (float) – learning rate
Returns:	the updated gradient.
Return type:	numpy.array

class theta.gradientschemes.adam(b1=0.9, b2=0.999, epsilon=1e-08)¶

The Adam scheme.

Parameters:	b1 (float) – weight of the previous first moment of the gradient estimate b2 (float) – weight of the previous second moment of the gradient estimate epsilon (float) – smoothing term to avoid division by zero

getupdate(G, lr)¶

Get updates.

Parameters:	G (numpy.array) – gradients lr (float) – learning rate
Returns:	the updated gradient.
Return type:	numpy.array

Activations¶

All activations functions are inherited from the theta.activations.actfunc class, so custom activations can be implemented by extending that class.

The current code contains the following activation functions:

Linear¶

class theta.activations.linear¶

A linear pass through.

static activation(x)¶

Evaluates the activation function.

Parameters:	x (numpy.array) – the input data.
Returns:	the activation function evaluation.
Return type:	numpy.array

static gradient(x)¶

Evaluates the gradient of the activation function.

Parameters:	x (numpy.array) – the input data.
Returns:	the gradient of the activation function.
Return type:	numpy.array

Sigmoid¶

class theta.activations.sigmoid¶

The sigmoid activation.

static activation(x)¶

Evaluates the activation function.

Parameters:	x (numpy.array) – the input data.
Returns:	the activation function evaluation.
Return type:	numpy.array

static gradient(x)¶

Evaluates the gradient of the activation function.

Parameters:	x (numpy.array) – the input data.
Returns:	the gradient of the activation function.
Return type:	numpy.array

Tanh¶

class theta.activations.tanh¶

The tanh activation.

static activation(x)¶

Evaluates the activation function.

Parameters:	x (numpy.array) – the input data.
Returns:	the activation function evaluation.
Return type:	numpy.array

static gradient(x)¶

Evaluates the gradient of the activation function.

Parameters:	x (numpy.array) – the input data.
Returns:	the gradient of the activation function.
Return type:	numpy.array

Custom activation functions can be implemented by extending the theta.activations.actfunc class.

Initializers¶

All initializers are inherited from the theta.initializers.initializer class, so custom initializers can be implemented by extending that class.

The current code contains the following parameter initalizers:

Uniform¶

class theta.initializers.uniform(bound=1, center=0)¶

Uniformly distributed initialization.

Parameters:	bound (float) – half-width of the distribution [-bound,+bound] center (float) – location of the center

Normal¶

class theta.initializers.normal(mean=0, sdev=1)¶

Normal distribution initialization.

Parameters:	mean (float) – mean of the normal distribution sdev (float) – standard deviation

Null¶

class theta.initializers.null¶: Initialize all parameters to zero.

Glorot normal¶

class theta.initializers.glorot_normal¶: Initializes with glorot normal distribution.

Glorot uniform¶

class theta.initializers.glorot_uniform¶: Initializes with glorot uniform distribution.

Custom initalization schemes can be easily implemented by extending the theta.initializers.initializer class.

Cost functions¶

All cost functions are inherited from the theta.costfunctions.costfunction class, so custom costs can be implemented by extending that class.

The current code contains the following cost functions:

MSE¶

class theta.costfunctions.mse¶: Mean squared error

Logarithmic¶

class theta.costfunctions.logarithmic¶: Logarithmic total cost

Sum¶

class theta.costfunctions.sum¶: Sum total cost

RMSE¶

class theta.costfunctions.rmse¶: Root mean squared error

Stopping conditions¶

The stopping condition can be used with the theta.minimizer.SGD minimizer. The validation data is monitored and if a specific condition is achieved the optimization is stopped. Custom stopping conditions can be implemented by extending the theta.minimizer.stopping abstract class.

The current code contains the following stopping algorithms:

Early Stop¶

class theta.stopping.earlystop(delta=10)¶

A simple implementation of early stopping. If the validation loss function increases after delta iterations the stop signal is send to the minimizer.

Parameters:	delta (int) – the number of iterations to pass until the stopping condition check becomes active.

do_stop(v)¶

Function which tests if the stop condition is reached.

Parameters:	v (numpy.array) – history of the validation loss function.
Returns:	True if the validation loss is growing in the delta window, False elsewhere.
Return type:	bool